En el caso general de un sistema de fuerzas en el espacio, el sistema equivalente fuerza-par en O consta de una fuerza R y un vector de par Mf), ambos distintos de cero, que no son perpendiculares entre sí (figura A).
Por tanto, el sistema de fuerzas no puede ser reducido a una sola fuerza o a un solo par. Sin embargo, el vector de par puede ser reemplazado por otros dos vectores de par obtenidos al descomponer Mq en una componente M| a lo largo de R v una componente M¡> en un plano perpendicular a R (figura B).
Entonces, el vector de par M2 y la fuerza R pueden reemplazarse por una sola fuerza R que actúa a lo largo de una nueva línea de acción. Por tanto, el sistema original
de fuerzas se reduce a R y al par vector M1 (figura C)
De esta forma, el sistema se reduce a R y un par que actúa en el plano perpendicular a R, a este sistema fuerza-par, en particular, se le conoce como llave de torsión debido a que la combinación resultante de empuje y torsión es la misma.
Por tanto, el paso de una llave de torsión puede ser expresado como:
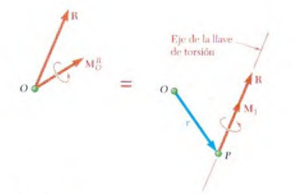
Para definir el eje de una llave de torsión se puede escribir una relación
que involucre al vector de posición r de un punto arbitrario P
localizado sobre dicho eje. Fijando la fuerza resultante R y el vector
de par M, en P (figura) y expresando que el momento con respecto
a O de este sistema fuerza-par, es igual al momento resultante
Mo del sistema original de fuerzas, se escribe
M, + r x R = Mo






No hay comentarios:
Publicar un comentario