sistema equivalente que se considera irreductible (mínimo en sus componentes) que
produzca los mismos efectos externos que el sistema original.
Los sistemas irreductibles son:
a) el constituido por una sola fuerza:
Los sistemas de fuerzas que pueden reducirse a una sola fuerza son los colineales, concurrentes (coplanares y espaciales), paralelos y generales en el plano.En este tipo de reducción se consideran dos posibilidades:
a.1) la reducción consiste en una fuerza que pasa por el origen del sistema de
referencia. Las coordenadas vectoriales del sistema por reducir son:
a.2) la reducción consiste en una fuerza cuyo soporte no pasa por el origen
del sistema de referencia. Cuado las coordenadas vectoriales del sistema
por reducir son:
tendremos para estas condiciones existen dos posibilidades:
a.2.1.) que el momento MO y la fuerza F sean perpendiculares
resumiendo
b) a.2.2 ) el constituido por una fuerza y un par no coplanares (motor)
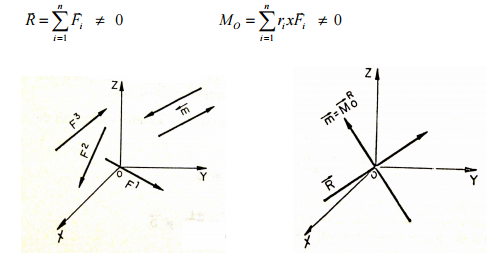
Los sistemas de fuerzas que pueden reducirse a una fuerza y un par no
coplanares son los sistemas generales en el espacio, siempre y cuando no
sean reductibles a una fuerza, a un par de fuerzas o al equilibrio y cuando
las coordenadas vectoriales canónicas sean :
y además se cumple que R • MO ≠ 0, es decir, estos vectores no son
perpendiculares.

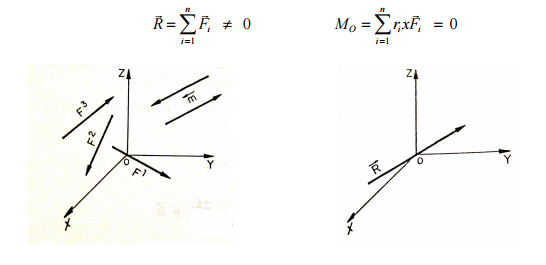



fuck
ResponderEliminar