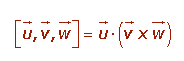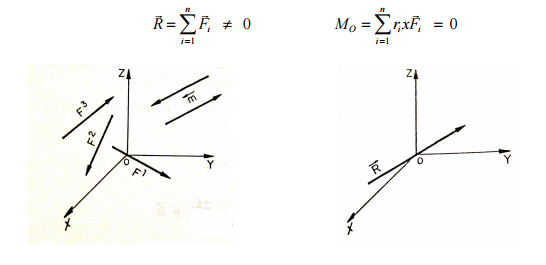Inicio

3.1 Introducción

    Al definir que un cuerpo rígido es aquel que no se de forma, se supone que la mayoría de los cuerpos considerados en la mecánica elemental son rígidos. Sin embargo, las estructuras y máquinas rea les nunca son absolutamente rígidas y se deforman bajo la acción de las cargas que actúan sobre ellas. A pesar de ello, por lo general esas de formaciones son pequeñas y no afectan las condiciones de equilibrio o de movimiento de la estructura en consideración. No obstante, tales deformaciones son importantes en lo concerniente a la resistencia a la falla de las estructuras y están consideradas en el estudio de la mecánica de materiales.

    En este capítulo se estudiará el efecto de las fuerzas ejercidas sobre un cuerpo rígido y se aprenderá cómo reemplazar un sistema de fuerzas dado por un sistema equivalente más simple. Este análisis estará basado en la su posición fundamental de que el efecto de una fuerza dada sobre un cuerpo rígido permanece inalterado si dicha fuerza se mueve a lo largo de su línea de acción (principio de transmisibilidad). Por tanto, las fuerzas que actúan sobre un cuerpo rígido pueden representarse por

vectores deslizantes.

.

    Dos conceptos fundamentales asociados con el efecto de una fuerza sobre un cuerpo rígido son el momento de una fuerza con respecto a un punto y el momento de una fuerza con respecto a un eje. Como la determinación de estas cantidades involucra el cálculo de productos escalares y vectoriales de dos vectores, en este capítulo se presentarán los aspectos fundamentales del álgebra vectorial aplicados a la solución de problemas que involucran fuerzas que actúan sobre cuerpos rígidos.

    Otro concepto que se presentará en es te capítulo es el de un par, esto es, la combinación de dos fuerzas que tienen la misma magnitud, líneas de acción paralelas y sentidos opuestos. Como se verá, cual quier sistema de fuerzas que actúa sobre un cuerpo rígido puede ser reemplazado por un sistema equivalente que consta de una fuerza, que actúa en cierto punto, y un par. Este sistema básico recibe el nombre de sistema fuerza-par. En el caso de fuerzas concurrentes, coplanares o paralelas, el sistema equivalente fuerza-par se puede reducirá una sola fuerza, denominada la resultante del sistema, o a un solo par, llamado el par resultante del sistema.

3.2 Fuerzas Externas e Internas

Las fuer zas que actúan sobre los cuerpos rígidos se pueden dividir en
dos grupos:

 1) fuerzas externas

         Las fuerzas externas representan la acción que ejercen otros cuerpos sobre el cuerpo rígido en consideración. Ellas son las responsables del comportamiento externo del cuerpo rígido. Las fuerzas externas causan que el cuerpo se mue va o aseguran que éste permanezca en reposo.
   

En la primera imagen se observa las fuerzas externas que se aplica al camión, mientas que en la segunda se observa mediante el DCL las fuerzas totales actuantes en el camión.


2) fuerzas internas.

       Las fuerzas internas son aquellas que man tienen unidas las partículas que conforman al cuerpo rígido. Si éste está constituido en su estructura por varias partes, las fuerzas que mantienen unidas a dichas partes también se definen como fuerzas internas.

3.3 Principio de Transmibilidad

    El principio de transmisibilidad establece que las condiciones de equilibrio o  de movimiento de un cuerpo rígido permanecerán inalteradas si una fuerza F que actúa en un punto dado de ese cuerpo se reemplaza por una fuerza F que tiene la misma magnitud y dirección, pe ro que actúa en un punto distinto, siempre y cuan do las dos fuerzas tengan la misma línea de acción). Las dos fuerzas, F y F , tienen el mismo efecto sobre el cuerpo rígido y se dice que son equivalentes. Es te principio establece que la acción de una fuerza puede ser transmitida a lo largo de su línea de acción, lo cual está basado en la evidencia experimental; no puede ser derivado a partir de las propiedades establecidas.

   Un ejemplo de esto es, si deseamos mover un cuerpo horizontalmente aplicando una fuerza, el resultado será el mismo si lo empujamos o si lo jalamos.

3.4 Producto Vectorial de dos Vectores

El momento de una fuerza con respecto a un punto se puede tomar como el producto vectorial de dos vectores.

El producto vectorial de los vectores P y Q se define como el vector V que satisface las siguientes condiciones:

 La línea de acción de V es perpendicular al plano que contiene a P y Q (figura a)

La magnitud de V es el producto de las magnitudes de P y Q por el se no del ángulo formado por P y Q (cuya medida siempre deberá ser menor o igual a 180°); por tanto, se tiene V=P.Qsen0

La dirección de V se obtiene a partir de la regla de la mano derecha.

Cierre su mano derecha y manténga la de manera que sus dedos estén doblados en el primer sentido que la rotación a través del ángulo que haría al vector P colineal con el vector Q; entonces, su dedo pulgar indicará la dirección del vector V. Obsérvese que si P y Q no tie nen un pun to de aplicación común, estos primeros se deben volver a dibujar a partir del mismo punto. Se di ce que los tres vectores P, Q y V (tomados en ese orden) forman una tríada a mano derecha.

Como se mencionó anteriormente, el vector V que satisface estas

tres condiciones (las cuales lo definen en forma única) se conoce como el producto vectorial de P y Q y se representa por la expresión matemática V=PxQ

En virtud de la notación utilizada, el producto vectorial de dos vectores P y Q también se conoce como el producto cruz de P y Q.

A partir de la ecuación se concluye que cuando dos vectores P y Q tienen la misma dirección, o direcciones opuestas, su producto vectorial es igual a cero. En el caso general, cuando el ángulo formado por los dos vectores no es 0° ni 180°, a la ecuación (3.1) se le puede dar una interpretación geométrica simple: la magnitud V del producto vectorial de P y Q es igual al área del paralelogramo que tiene como la dos a P y Q. Por tanto, el producto vectorial PxQ

permanece inalterado si Q se reemplaza por un vector Q que sea

coplanar a P y Q y tal que la línea que une a las partes terminales de

Q y Q sea paralelo a P. Así, se escribe V=PxQ=PxQ´

A partir de la tercera condición empleada para definir al producto vectorial V de P y Q, esto es, la condición que establece que P, Q y V deben formar una tríada a mano derecha, se concluye que los productos vectoriales no son comunitarios, es decir, Q P no es igual a P Q.

De hecho, se puede verificar fácilmente que Q P está representado por el vector V, que es igual y opuesto a V, entonces se escribe:

QxP (PxQ)

Ejemplo: Calcúlese el producto vectorial V=PxQ cuan do el vector P tiene una magnitud de 6 y se encuentra en el plano ZX que forma un ángulo de 30° con el eje x y el vector Q tiene una magnitud de 4 y se encuentra a lo largo del eje x.

A partir de la definición del producto vectorial se concluye que el vector V debe estar a lo largo del eje y, tener la magnitud:

V =PQsen0=(6)(4) sen 30°=12; y que debe estar dirigido hacia arriba.

3.5 Productos Vectoriales- Rectangulares

A continuación se procederá a determinar el producto vectorial de cualquier par de los vectores unitarios i, j y k, Considérese primero el producto ( I x J )....(figura A).

     Como ambos vectores tienen una magnitud igual a 1 y dado que éstos forman ángulos rectos entre sí, su producto vectorial también deberá ser un vector unitario. Dicho vector unitario debe ser k, puesto que los vectores i, j y k son mutuamente perpendiculares y forman una tríada a mano derecha. Por otra parte, a partir de la regla de la mano derecha presentada, se concluye que el producto ( J x I ) debe ser igual a k (figura B). Por último, se debe observar que el producto vectorial de un vector consigo mismo, como(I x I) es igual a cero debido a que ambos vectores tienen la misma dirección.

  

Los productos vectoriales para los diversos pares posibles de vectores unitarios son:

     Si se ordena las tres letras que representan a los vectores unitarios en un círculo en sentido contrario al movimiento de las manecillas del reloj (figura3.11) se puede facilitar la determinación del signo del producto vectorial de dos vectores unitarios: el producto de dos vectores unitarios será positivo si éstos se siguen uno a otro en un orden contrario movimiento de las manecillas del reloj y será negativo si éstos se siguen uno al otro en un orden en el sentido de las manecillas del reloj.

3.6 Momento de una Fuerza Respecto a un Punto

     El momento de F con respecto a O se define como el producto vectorial de r y F:

Mo=r x F

     El momento MO debe ser perpendicular al plano que contiene el punto O y a la fuer za F. El sentido de MO está definido por el sentido de la rotación que haría al vector r colineal con el vector F.

    En el sistema de unidades del SI, donde la fuerza se expresa en newtons (N) y la distancia se expresa en metros (m), el momento de una fuerza estará expresado en newtons-metro (N m). 

   En el sistema de unidades de uso común en Estados Unidos, donde la fuerza se expresa en libras y la distancia en pies o en pulgadas, el momento de una fuerza se expresa en lb ft o en lb in.

    Se puede observar que a pesar de que el momento MO de una fuerza con respecto a un punto depende de la magnitud, la línea de acción y el sentido de la fuerza, dicho momento no depende de la posición que tiene el punto de aplicación de la fuerza a lo largo de su línea de acción.

3.7 Teorema de Varignon

   La propiedad distributiva de los productos vectoriales se puede emplear para determinar el momento de la resultante de varias fuerzas concurrentes. Si las fuer zas F1, F2, . . . se aplican en el mismo punto A y si se representa por r al vector de posición A, a partir de la ecuación se puede concluir que

 r (F1+F2+....)=r x F1 + r x F2....

    Esto es, el momento con respecto a un punto dado O de la resultante de varias fuerzas concurrentes es igual a la suma de los momentos de las distintas fuerzas con respecto al mismo punto O.

Ejemplo:

3.8 Componentes Rectangulares

    En general, la determinación del momento de una fuerza en el espacio se simplifica en forma considerable si el vector de fuerza y el vector de posición a partir de su punto de aplicación se descomponen en sus componentes rectangulares x, y y z. Por ejemplo, considere el momento Mo con respecto a O de una fuerza F con componentes Fx, Fy y Fz que está aplicada en el punto A de cooredenads x, y y z.

Se observa que las componentes del vector de posición r son iguales, respectivamente, a las cooredenadas x, y y z del punto A, se escribe

r = xi + yj + zk -----> (3.15)

F = Fxi + Fyj + Fzk ------> (3.16)

Al sustituir a r y a F a partir de (3.15) y (3.16) en

Mo = r X F

se puede escribir el momento Mo de F con respecto a O de la siguiente forma

Mo = Mxi + Myj + Mzk

donde las componentes escalares Mx, My y Mz están definidas por las relaciones:

3.9 Producto Escalar de dos Vectores

    El producto escalar de dos vectores P y Q se definen como el producto de las magnitudes de P y Q y el coseno del angulo teta formado por P y Q. El producto escalar de P y Q se denota mediante P ·Q.

 Entonces se escribe P · Q = PQ coseno teta. 

3.10 Producto Triple Mixto de Vectores

    El producto mixto de los vectores vector u,  y w es igual al producto escalar del primer vector por el producto vectorial de los otros dos.

El producto mixto se representa por [vector u, , w].

      El producto mixto de tres vectores es igual al determinante que tiene por filas las coordenadas de dichos vectores respecto a una base ortonormal.

3.11 Momento de una Fuerza con respecto a un Eje

    La fuerza que se aplica a un eje en particular cuanta con un brazo de palanca el cual se considera que es la distancia perpendicular que hay de la línea de acción de la fuerza al eje de rotación, este determina la eficacia de una fuerza dada para provocar el movimiento de rotación.

Ejemplos de ello lo son:

• Si se ejerce una fuerza de 20 N sobre un cable enrollado alrededor de un tambor de 120 mm.¿Cuál es el momento de torsión producido aproximadamente al centro del tambor?

Solución:

  Note que la línea de acción de la fuerza de 20 N es perpendicular al diámetro del tambor. Por lo tanto, el brazo de palanca es igual al radio del tambor. Si se convierte el diámetro a metros (0.12m), el radio es de 0.06 m. El momento de torsión se calcula:

T= F x r =-(20 N) (0.06 m)= -1.20 N . m

Resultado=-1.20 N.m

*Nota:

El momento de torsión es negativo porque tiende a causar una rotación en el  sentido contrario a las manecillas del reloj.

3.12 Momento de un Par

   Las fuerzas que no tienen una línea de acción común producen una resultante del momento de torsión, además de una resultante de la fuerza traslacional. Cuando las fuerzas aplicadas actúan en el
mismo plano, el momento de torsión resultante es la suma algebraica de los momentos de torsión  positivos y negativos debido a cada fuerza.

Ejemplo:

Determinar el momento de torsión resultante en A debido a las fuerzas de 60 N y 80 N de la siguiente figura:

Solución:

Se traza un diagrama de cuerpo libre y se construyen los brazos de palanca r1 y r2. La longitud de los brazos de palanca son:

r1= (12 cm) sen 50 = 9.19 cm
r2= (10 cm) sen 70= 9.40 cm

Si se considera A como eje de rotación. El momento de torsión debido a F1 es negativo y el causado por F2 es positivo. El momento de torsión resultante se encuentra así:

tR= t1 + t2= F1r1 + F2r2

=-(60 N)(9.19 cm)+(80N)(9.40cm)

=-552 N . cm + 752 N . cm

=200 N . cm

*Resultado= momento de torsión resultante 2 N . m

3.13 Pares Equivalentes

    Cualquier fuerza F que actúa en un punto A de un cuerpo rígido puede reemplazarse por un sistema fuerza-par en un punto arbitrario O el cual consta de la fuerza F aplicada en O y un par de momento Mo, igual al momento de la fuerza F en su posición original con respecto a O; se debe señalar que la fuerza F y el vector de par M0 siempre son perpendiculares entre sí.

  Para que un par se equivalente a otro se debe cumplir:

 • Magnitud del momento resultante igual

 • Sentido de giro del momento el mismo. 

• Estar en planos paralelos

3.14 Adición de Pares

Solamente se pueden sumar pares si sus fuerzas son concurrentes o sus líneas de acción se cruzan en algún punto.

Considere dos planos P1 y F2 que se intersecan y dos pares que actúan, respectivamente, en P¡ y P2. Se puede suponer, sin perder la generalidad, que el par en Pi consta de dos fuerzas F 1 y -F| perpendiculares a la línea de intersección de los dos planos y que actúan, respectivamente, en A y B (figura A).

 En forma similar, se supone que el par en P2 consta de dos fuerzas F 2 y -F2 perpendiculares a AB y que actúan, respectivamente, en A y B. Es obvio que la resultante R de F1 y F2 y la resultante -R de -F1 y -F2 forman un par. Si se representa con r el vector que une a B con A y si recordamos la definición de par, el momento M del par resultante queda expresado como sigue:

 M = r X R = r X (F| + F 2)

 y, por el teorema de Varignon:

 M = r X F1 + r X F2 

Pero el primer término en la expresión obtenida representa al momento Mj del par en P¡ y el segundo término representa al momento M2 del par en P2. Así se tiene M = M1 + M2 y se concluye que la suma de dos pares cuyos momentos son iguales a Mi y M2 es un par de momento M igual a la suma vectorial de M1 y M2 (figura B).

3.15 Representación de Pares en Vectores

Los pares que tienen el mismo momento, sin importar si actúan en el mismo plano o en planos paralelos, son equivalentes. Por tanto, no hay necesidad de dibujar las fuerzas que en realidad forman un par dado con el propósito de definir el efecto que dicho par tiene sobre un cuerpo rigido (Figura A)

 Es suficiente dibujar una flecha igual en magnitud y dirección al momento M del par (figura B) Por otra parte, quedó expresado que la suma de dos pares es otro par y que el momento M del par resultante puede obtenerse mediante la suma vectorial los momentos M] y M2, de los pares dados. Por consiguiente, los pares obedecen la ley para la adición de vectores y la flecha usada en la figura (B) para representar al par definido en la figura 3.38a puede considerarse como un vector verdadero.

3.16 Descomposición de una Fuerza en una Fuerza en O y un Par

   Considere una fuerza F que actúa sobre un cuerpo rígido en un punto A definido por el vector de posición r (figura A). Suponga que por alguna razón se quiere que la fuerza actúe en el punto O. Aunque F se puede mover a lo largo de su línea de acción (principio de transmisibilidad), no es posible moverla al punto O. que no se encuentra sobre la línea de acción original de la fuerza, sin modificar el efecto que F tiene sobre el cuerpo rígido.

   Sin embargo, pueden unirse dos fuerzas al punto O, una igual a F y otra igual a -F, sin modificar el efecto que la fuerza original tiene sobre el cuerpo rígido (figura B). 

Como una consecuencia de esta transformación, ahora una fuerza F se aplica en O; las otras dos fuerzas, forman un par con un momento

 M0 = r X F

   Por tanto, cualquier fuerza F que actúe .sobre un cuerpo rígido puede ser trasladada a un punto arbitrario O siempre y cuando se agregue un p ar cuyo momento sea igual al momento de F con respecto a O. El par tiende a impartirle al cuerpo rígido el mismo movimiento de rotación alrededor de O que la fuerza F ocasionaba antes de que fuera trasladada al punto O. El par se representa por el vector de par M0 que es perpendicular al plano que contiene a r y a F. Como M0 es un vector libre, puede ser aplicado en cualquier lugar; sin embargo, por conveniencia, usualmente el vector de par se fija en O, junto con F, y se hace referencia a la combinación obtenida como un sistema fuerza-par (figura C).

3.17 Reducción de un Sistema de Fuerzas a una Fuerza y un Par

  

Considérese un sistema de fuerzas F1, F2, F3, . . . que actúan sobre un cuerpo rígido en los puntos A1, A2, A3, . . . definidos por los vectores de posición r1, r2, r3, etc. (figura A).

 Como se vio en la sección anterior, F, puede ser trasladada de Ai a un punto dado O, si se agrega al sistema original de fuerzas un par de momento M1, igual al momento ri x F1 de F1 con respecto a O. Si se repite este procedimiento con F 2, F:i, . . . , se obtiene el sistema mostrado en la figura B, que consta de: las fuerzas originales, ahora actuando en O, y los vectores de par que han sido agregados.

 Como ahora las fuerzas son concurrentes, pueden ser sumadas vectorial mente y reemplazadas por su resultante R. De manera similar, los vectores de par M1, M2, M3, . . . pueden sumarse vectorialmente y ser reemplazados por un solo vector de par M ". Por tanto, cualquier sistema de fuerzas, sin importar qué tan complejo sea, puede ser reducido a un sistema equivalente fuerza par que actúa en un punto dado O (figura C). 

3.18 Sistemas Equivalentes de Fuerzas

    Dos sistemas de fuerzas son equivalentes si pueden ser reducidos al mismo sistema fuerza par en un punto dado O. El sistema fuerza para en O establece que dos sistemas de fuerzas F1, F2, F3 ... y F prima 1, F prima 2, F prima 3, ... que actúan sobre el mismo cuerpo rígido son equivalentes si y solo si, respectivamente, las sumas de las fuerzas y las de los momentos con respecto a un punto dado O de las fuerzas de los dos sistemas son iguales.

3.19 Sistemas Equipolentes de Fuerzas

 Si dos sistemas de fuerzas que actúan sobre un cuerpo rígido son equipolentes, entonces ambos también son equivalentes.

Es importante señalar que este enunciado no se aplica a cualquier sistema de vectores. Considérese, por ejemplo, un sistema de fuerzas que actúan sobre un conjunto independiente de partículas que no forman un cuerpo rígido. Es posible que un sistema de fuerzas diferentes que actúan sobre las mismas partículas pueda ser equipolente al primero, esto es, que dicho sistema tenga la misma resultante y el mismo momento resultante. Sin embargo, como ahora actuarán diferentes fuerzas sobre cada una de las partículas, los efectos de dichas fuerzas sobre estas partículas serán diferentes; en un caso similar, aunque los dos sistemas de fuerzas sean equipolentes, no son equivalentes.

3.20 Otras Reducciones de un Sistema de Fuerzas

Es el proceso que consiste en obtener, de un sistema de fuerzas cualquiera, un
sistema equivalente que se considera irreductible (mínimo en sus componentes) que
produzca los mismos efectos externos que el sistema original.

Los sistemas irreductibles son:

a) el constituido por una sola fuerza:

Los sistemas de fuerzas que pueden reducirse a una sola fuerza son los colineales, concurrentes (coplanares y espaciales), paralelos y generales en el plano.En este tipo de reducción se consideran dos posibilidades:


a.1) la reducción consiste en una fuerza que pasa por el origen del sistema de
referencia. Las coordenadas vectoriales del sistema por reducir son:

a.2) la reducción consiste en una fuerza cuyo soporte no pasa por el origen
del sistema de referencia. Cuado las coordenadas vectoriales del sistema
por reducir son:

 tendremos para estas condiciones existen dos posibilidades:

a.2.1.) que el momento MO y la fuerza F sean perpendiculares

 resumiendo

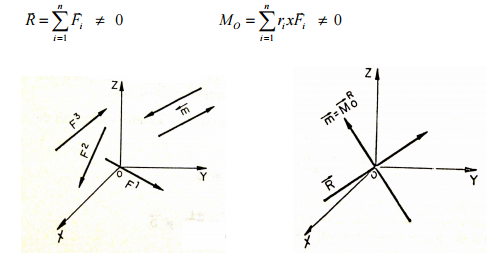
b) a.2.2 ) el constituido por una fuerza y un par no coplanares (motor) Los sistemas de fuerzas que pueden reducirse a una fuerza y un par no coplanares son los sistemas generales en el espacio, siempre y cuando no sean reductibles a una fuerza, a un par de fuerzas o al equilibrio y cuando las coordenadas vectoriales canónicas sean :

y además se cumple que R • MO ≠ 0, es decir, estos vectores no son perpendiculares.

3.21 Reducción De un Sistema de Fuerzas a una llave de Torsión

    En el caso general de un sistema de fuerzas en el espacio, el sistema equivalente fuerza-par en O consta de una fuerza R y un vector de par Mf), ambos distintos de cero, que no son perpendiculares entre sí (figura A).

 Por tanto, el sistema de fuerzas no puede ser reducido a una sola fuerza o a un solo par. Sin embargo, el vector de par puede ser reemplazado por otros dos vectores de par obtenidos al descomponer Mq en una componente M| a lo largo de R v una componente M¡> en un plano perpendicular a R (figura B). 

Entonces, el vector de par M2 y la fuerza R pueden reemplazarse por una sola fuerza R que actúa a lo largo de una nueva línea de acción. Por tanto, el sistema original

de fuerzas se reduce a R y al par vector M1 (figura C)

   De esta forma, el sistema se reduce a R y un par que actúa en el plano perpendicular a R, a este sistema fuerza-par, en particular, se le conoce como llave de torsión debido a que la combinación resultante de empuje y torsión es la misma.

Por tanto, el paso de una llave de torsión puede ser expresado como:

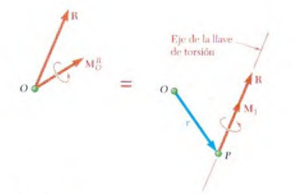
 Para definir el eje de una llave de torsión se puede escribir una relación que involucre al vector de posición r de un punto arbitrario P localizado sobre dicho eje. Fijando la fuerza resultante R y el vector de par M, en P (figura) y expresando que el momento con respecto a O de este sistema fuerza-par, es igual al momento resultante Mo del sistema original de fuerzas, se escribe M, + r x R = Mo